據北京大學微信號消息，今年春晚，魔術師劉謙表演了一個與紙牌相關的魔術，精妙的設計帶給觀眾極高的參與感，許多人紛紛拿出家中的撲克牌，跟著劉謙一起“見證奇跡”。“小尼的撲克牌沒對上”也登上了熱搜。

這個魔術“奇跡”的背后

有著怎樣的奧秘？

當春晚還在進行中，北京大學數學科學學院2021級本科生劉明昊、李新宇、殷子縈，2022級本科生王秭如、黃天銘、王美潭，2023級本科生潘浩翔、王偉圣便寫出一篇科普文章，從數學的角度帶大家感受這一魔術的魅力。

魔 術 步 驟

首先，準備4張撲克牌，跟隨魔術步驟，來一起“見證奇跡”。

魔 術 揭 秘

怎么樣，你的撲克牌對上了嗎？下面，幾位北大同學將按照步驟順序一步步為你揭秘背后的邏輯

步驟一

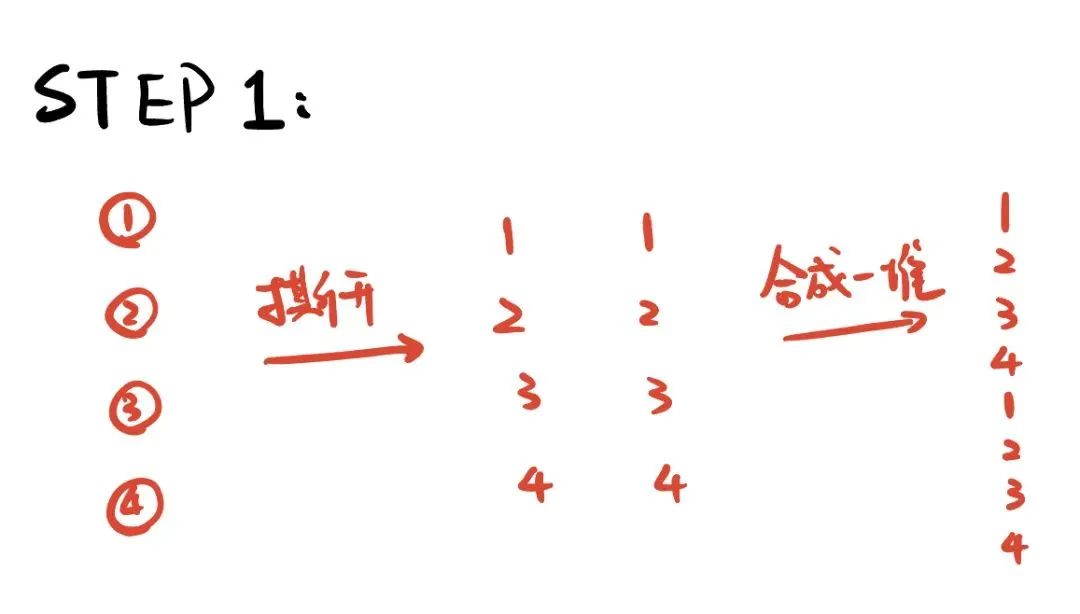
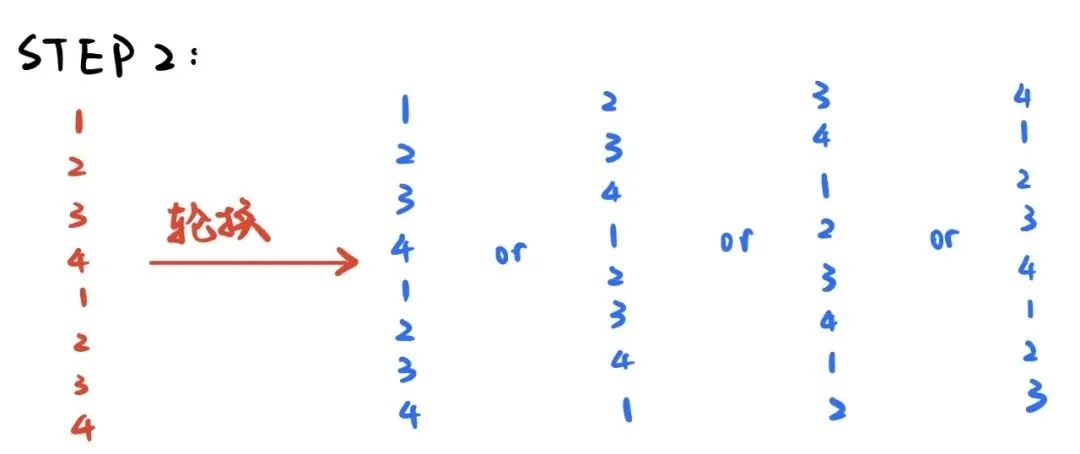
我們令選擇的四張撲克牌分別為1234，將他們分別撕開后，產生了標號分別為1234的兩套（半張）撲克牌，疊在一起后形成了從上至下標號分別為12341234的撲克牌堆。

步驟四

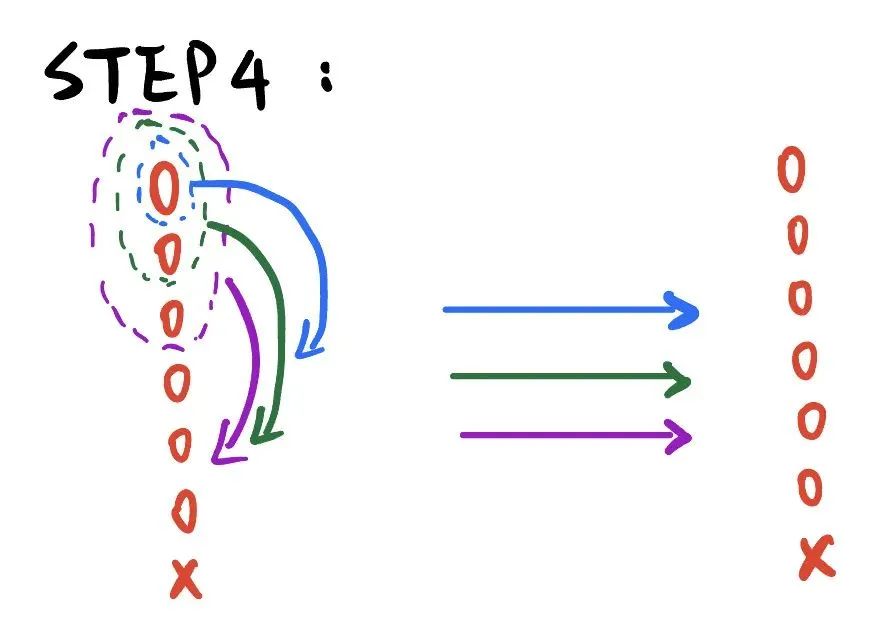
在上一步之后，牌堆的編號為000000X，于是，無論本輪中選擇牌堆頂多少張牌插入牌堆中，都不會影響目標牌的位置，仍然處于牌堆底部。

步驟五

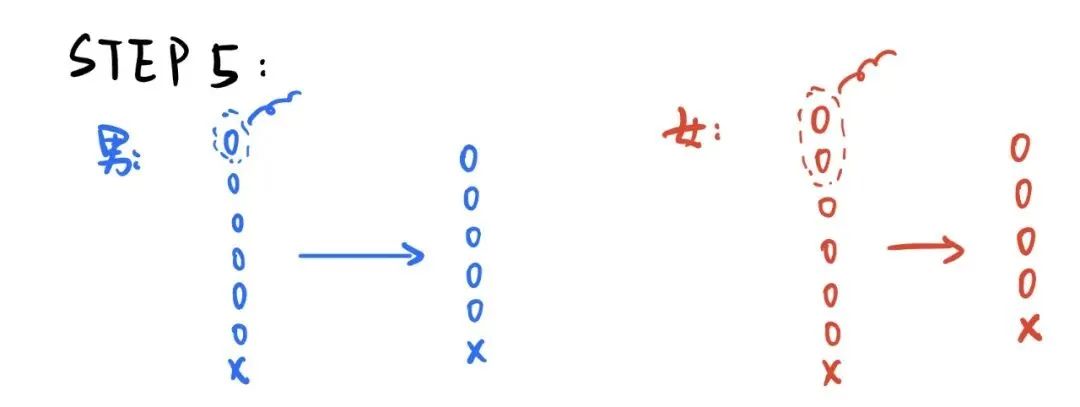
此時男生的牌堆為：00000X

女生的牌堆為：0000X

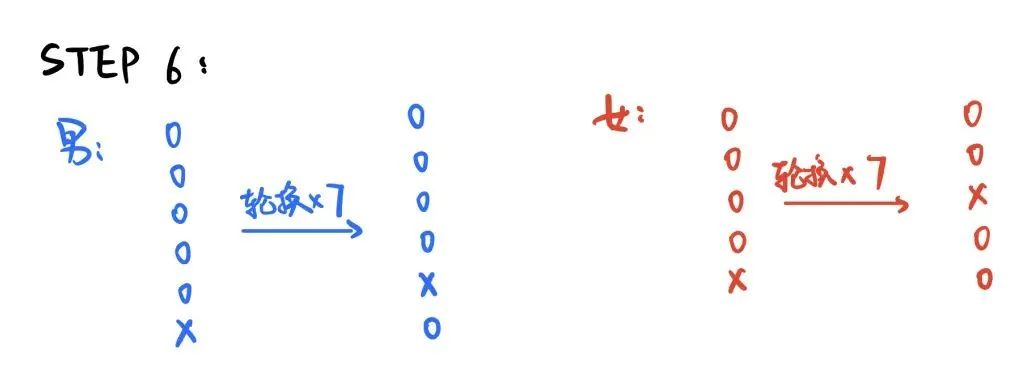
步驟六

通過嘗試可知，在經過步驟六后將得到如下的牌堆：

男生：0000X0

女生：00X00

步驟七

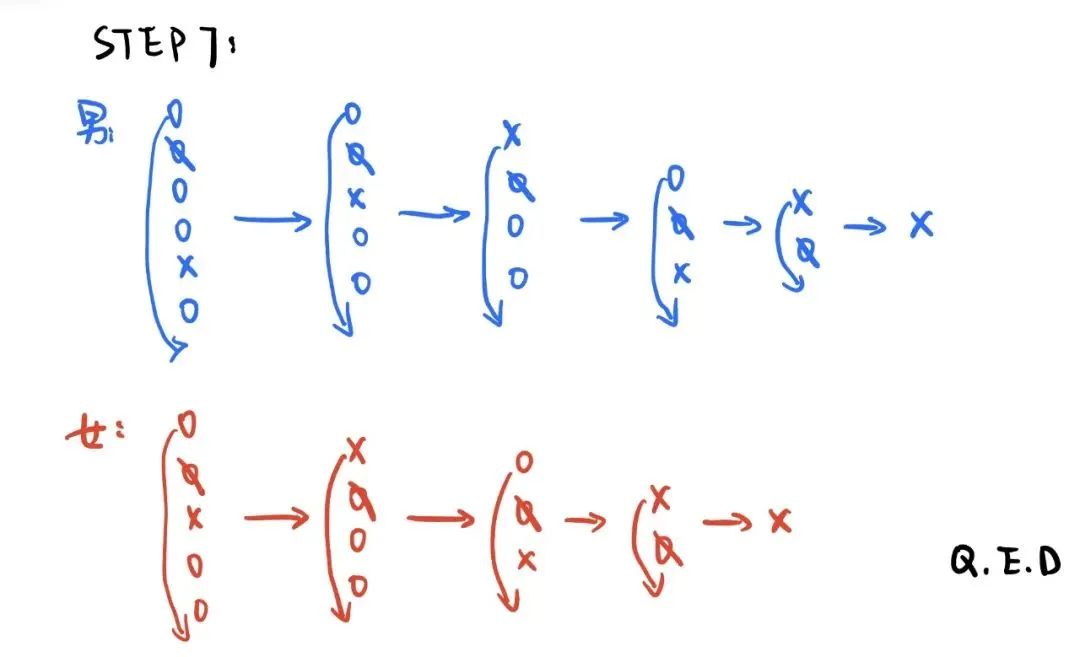
通過上述揭秘

相信大家不難看出

這個魔術的背后

其實是一個數學上的問題

它被稱為約瑟夫問題

約瑟夫問題

設有編號為1，2，......，n的n個人圍成一個圈，從第1個人開始報數，報到m時停止報數，報m的人出圈。再從他的下一個人起重新報數，報到m時停止報數，報m的出圈......按照這個規則進行下來，直到所有人全部出圈為止。求最后留下來的人編號。

為了使問題簡化，我們考慮n個人編號為0 ~ n-1的情況，每 m 個人退出一個人，我們稱之為（n, m）問題。

第一個人（即編號為在模n下同余m的人）退出之后，對剩下的 n-1 個人重新編號，則新問題的k號在原問題中對應 k+m 號。因此（n, m）問題的解 J (n, m) = J (n-1, m)+m 且 J (1, m) = 1（模n意義下）。據此，通過遞推的方法可以得到 J (n, m)。

在實踐中，約瑟夫問題一般用代碼進行求解。劉謙的魔術中使用的便是 m=2 的特殊情況。

那么主持人小尼

為什么失敗了呢？

一起來看看背后的原因

根據上面的證明過程，我們不難發現：在步驟3與步驟4中，如果操作正確，每位主持人手中最底部的一張牌沒有變化，而這恰好是步驟7后留下的一張牌。

然而，在進行步驟4時，注意尼格買提的手上動作：

鏡頭捕捉到插入過程中，原本位于底部的牌面花紋被另一張牌覆蓋，也就是說，尼格買提并未按要求將兩張牌放入中間位置，從而導致他最終匹配的失敗。

聽完北大同學的講解，你理解魔術背后的數學問題了嗎？